INTERNAL HYDRATION OF BACTERIORHODOPSIN  Sophia Yancopoulos,  Mihaly Mezei, Roman Osman Originally  presented as poster 210 February, 2001 at  Annual Biophysical Society Meeting  in Boston, MA

click for MMC

The recent crystallographic structures of the D96N mutant of bacteriorhodopsin (Luecke et al, 1999)in the ground (BR) and the excited (M) states reveal internal waters with proposed specific functionality. We have investigated the localization of the internal waters with grand canonical ensemble Monte Carlo simulations. The most probable positions of simulation sites were determined with the generic site method. The results of the simulations show 3 clusters of internal sites in each state and additional isolated sites in hydrophobic pockets. Ten of the 11 internal BR state waters are well matched by the simulations at an occupancy-weighted average distance of 0.69 ± 0.5 A. Three additional internal sites with total occupancy of 1.71 have been found for the BR state and 11 additional in the M state with total occupancy of 6.4 waters. Superimposing the two data sets yields 14 water pairs with an average distance of 0.82 ± 0.45 A. The simulation locates only one of three missing waters near Asn-96 in the M state.Supported by Training Grant DK07645
 
 
 

INTRODUCTION
 
 

Water is an in integral component of proteins and plays an important role in their structure and function. High resolution structures determined by x-ray crystallography have recently become available for bacteriorhodopsin, a 7 TM protein, and its mutants (Luecke et al, 1999). The waters in these structures have been clearly observed and offer an excellent opportunity to test theoretical methods of solvation. Furthermore, simulations offer an opportunity to investigate the properties of internal waters and their role.
 

METHODS
 
 

In order to explore the placement of water in the transmembrane domain of the 7 TM protein bacteriorhodopsin we have used a Grand Canonical Ensemble Metropolis Monte Carlo (MMC) cavity biased insertion method (Resat and Mezei, 1994). This method has already been successful in determining water positions in a number of crystal structures, for example,  small polydisaccharides (Resat & Mezei, 1994),  DNA (Resat & Mezei, 1996), and  complexes of inhibitors bound to HIV-1 protease (Marrone et al.1998). The cavity-biased formulation of MMC was chosen since it improves statistical sampling efficiency (Mezei 1987) and is therefore an appropriate method to investigate the solvation of the TM domain of BR.
 

Cavity Biased GRAND CANONICAL ENSEMBLE MMC
 

In this approach the insertion of a molecule is attempted if a cavity of appropriate radius is found and accepted with a probability:
 
 

where E(N) is the potential energy of the system of N particles and P_cav(N) is the probability of finding a cavity of a specific size.

The parameter B is related to the excess chemical potential as

Where <N> is the average over the number of particles.
 
 

TUNING THE B PARAMETER
 
 

The scheme is implemented by first adjusting the  B parameter  until the targeted number of molecules of solvent is approximately achieved outside a rectangular region containing the  molecule so that the density in this region external to the protein approaches the density of water (0.997 grams per cc).  Water molecules are then inserted or deleted by accepting or rejecting each attempt based on the Metropolis Monte Carlo criterion.

The tuned values of the B parameter were respectively: -1.2 and ?1.35 for the BR and M states.
 

CALCULATION:
 

The atomic coordinates of the BR (unphotolyzed) state, observed at 1.8 Angstrom resolution, and M (excited) state observed with a resolution of 2Å, from the Protein Data Bank (accession numbers 1C8RR and 1C8S respectively). The waters and lipids were removed from the structures.  Hydrogens were added to the structures with CHARMM. The N-and C-termini as well as two residues, which were discontinuous in the original structures, were capped with acetyl and N-methyl groups, respectively.

The BR and M states were run for  5 million and 6 million MMC steps, respectively, with the equilibrated B parameter. The coordinates of the atoms in the systems were stored every 10,000 steps during sampling.  During the simulations the solute residues were kept fixed at their experimental crystal structures and only the water molecules were allowed to move. This was in keeping with prior MMC simulations (Resat and Mezei 1996). Periodic boundary conditions were applied with the cell size as determined by simulaidês OPT. The temperature was 298 K. The water model chosen was the TIP3P (Jorgensen et al., 1983) with the solute potential type calculated in CHARMM.  The solute-solvent cutoff was used with the minimum-image convention. The solvent spherical cutoff was 10 Å.  The resultant average densities obtained in the exterior region were  0.99875 g/ml and 0.99743 g/ml respectively  in the BR and M states.
 

LOCATING GENERIC SITES:
 

To establish the positions of water sites from the simulation,  we utilized the generic solvent (GS) site method developed by Mezei and Beveridge, 1984.  The configurations from the trajectory are superimposed and the generic sites are determined by the graph theoretical  method, (Berge, 1962), which minimizes the root mean square deviation between the GS and the individual waters assigned to it in each snapshot.  The GS are characterized by  mean locations for the oxygen positions, the mean square deviation of the position, and the occupancy of the site: the ratio of the number of water molecules assigned to the location divided by the total number of configurations.
 
 

                                                                                                         Table 1a: Internal BR State Generic Sites matching  Crystallographic Waters

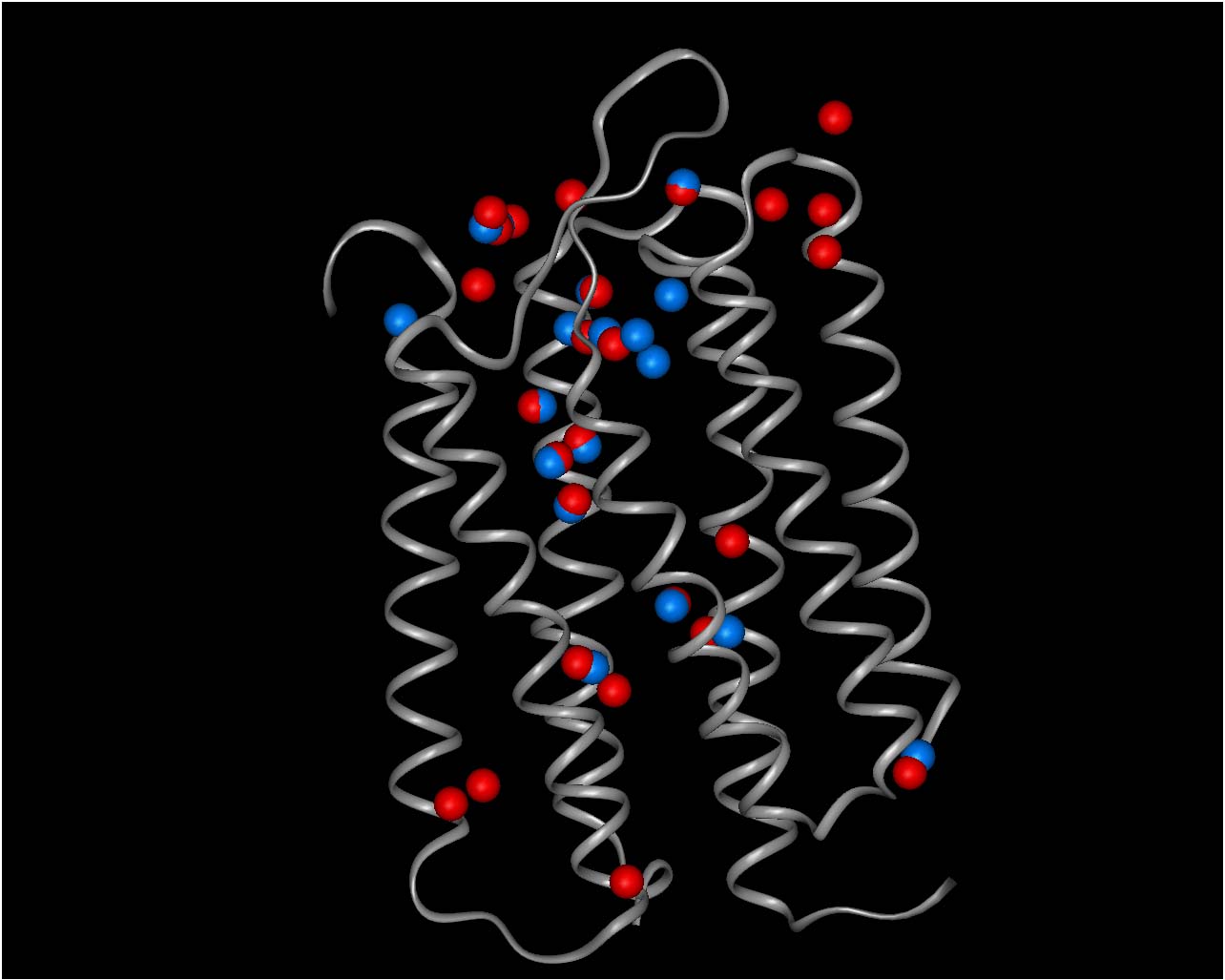
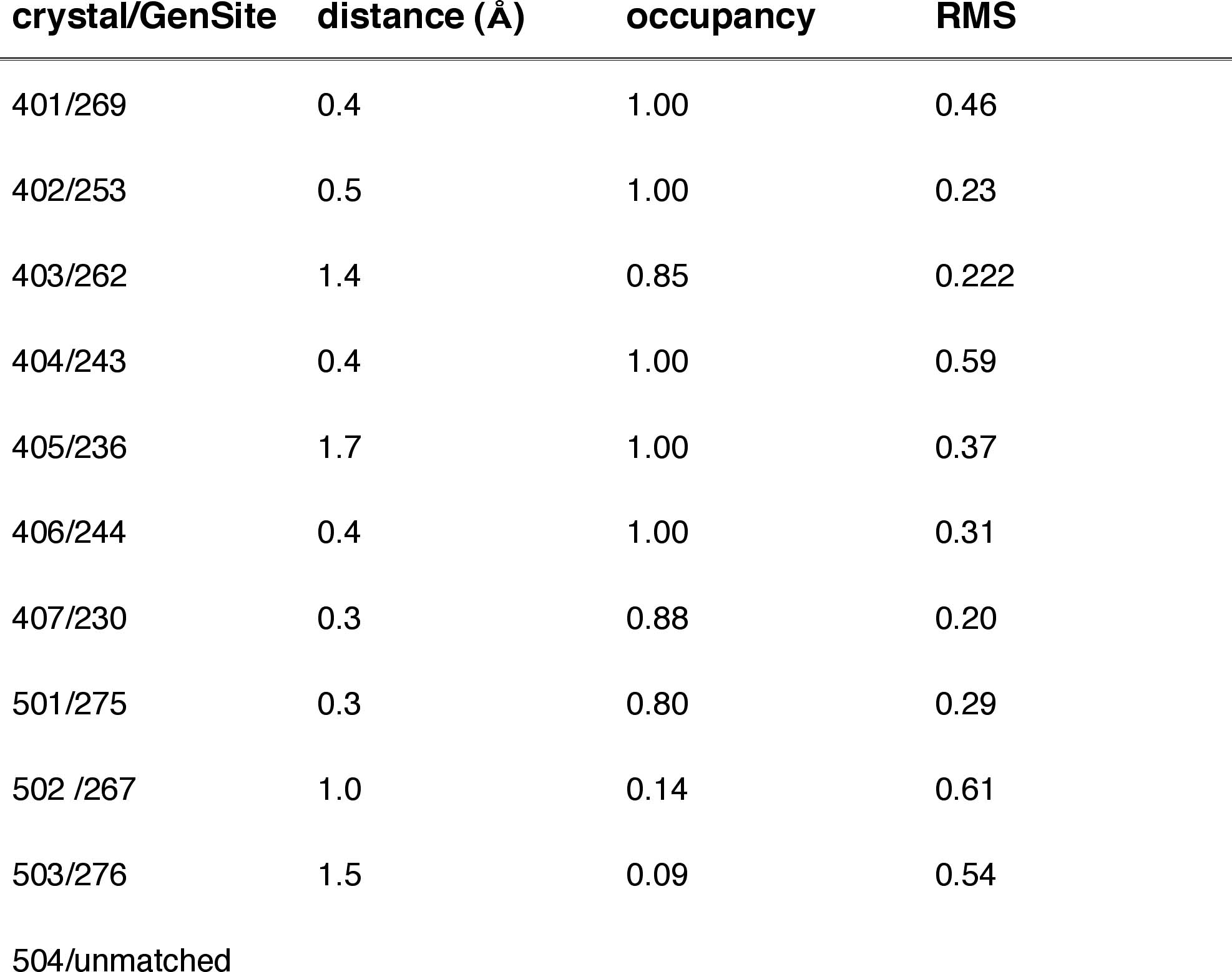
Figure 1.(blue) BR state simulation waters  superimposed on
           (red) X-ray positions.
 
 

• Ten of the eleven internal BR state data waters  are well matched by  the MMC simulations with an average distance weighted by occupancy of 0.69 Å and standard deviation of 0.5 Å.

• GS sites matching Crystallographic waters 502 and 503 were observed with low occupancy and no matching GS for water 504 was observed.

EXPLANATION FOR MISSING AND LOW OCCUPANCY WATERS:
 

Two factors influence the occupancy of a site. One is the potential energy of the water at a particular insertion site. The other is the B factor, which controls the equilibration between the excess chemical potential and the average number of particles in the GC ensemble.
 
 

  Energies of Representative Sites in k-cal/mol

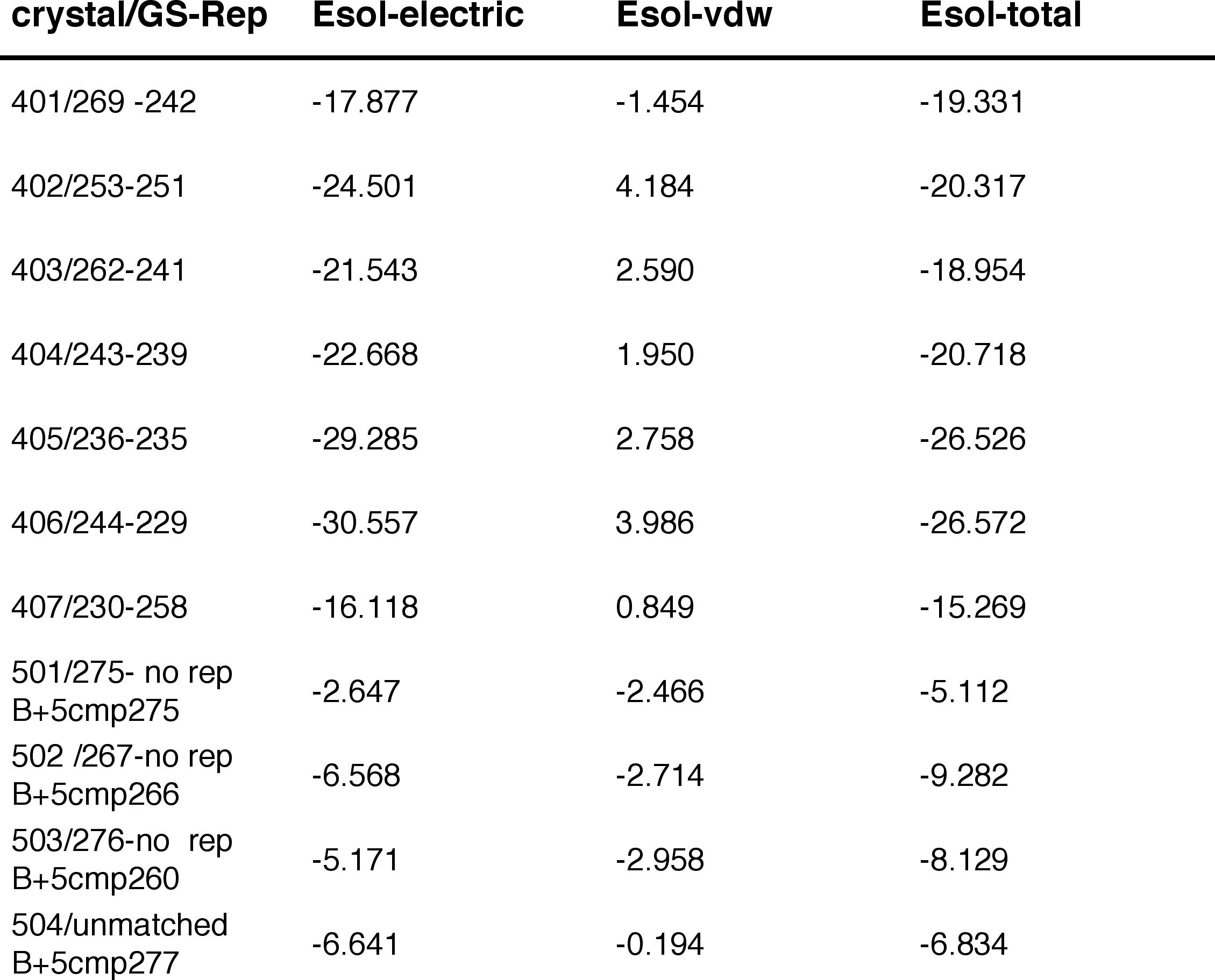
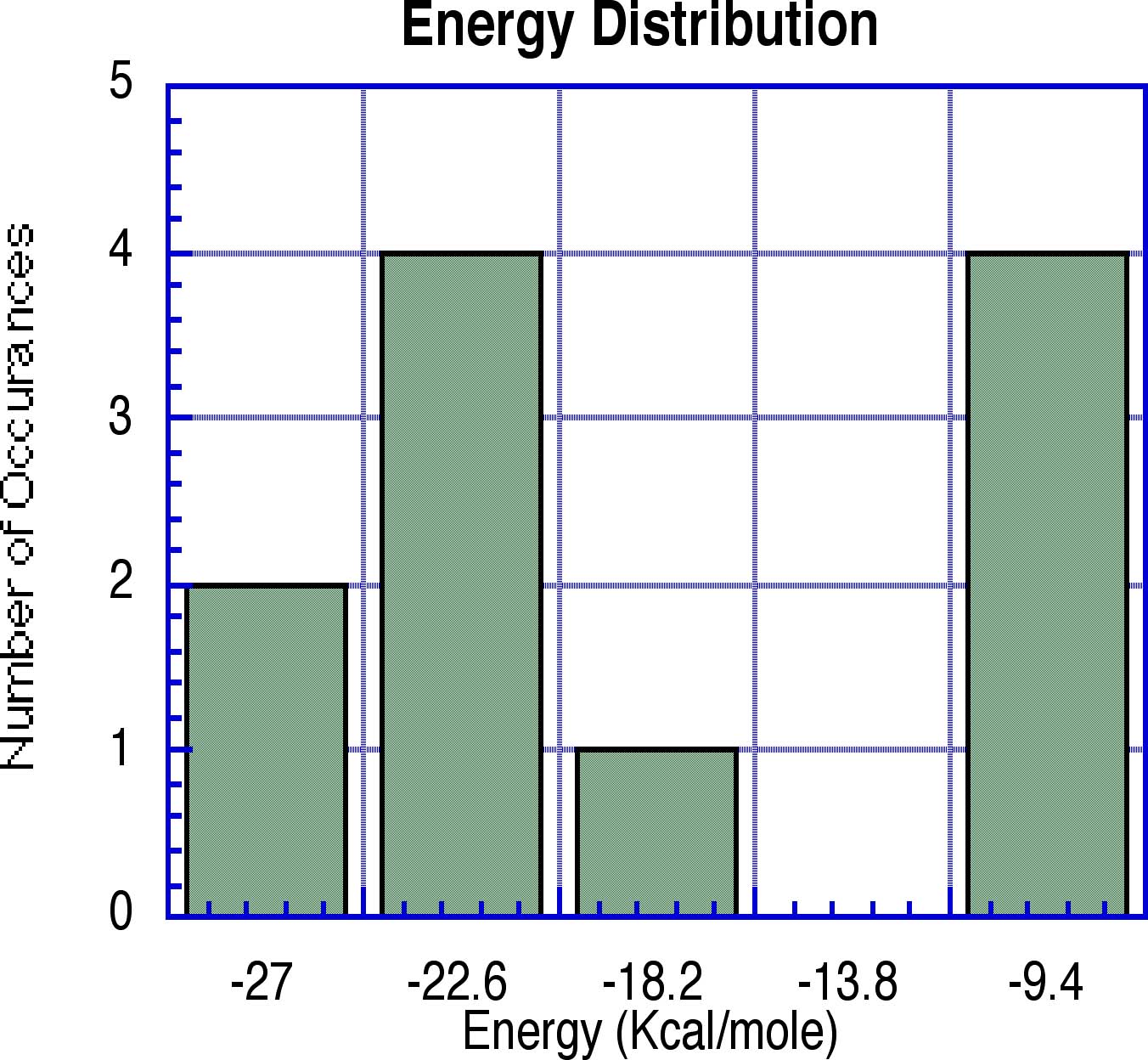
Conclusion: Waters in low occupancy sites have significantly higher energies.
 
 
 

                        Occupancy as a function of B:

Increasing the excess chemical potential (i.e., increasing B) progressively increases the  occupancy by overcoming the unfavorable energy.
 
 
 

Simulations find Additional Waters:
 

                                                                                                      Table 1b: Internal BR Generic Sites withoutmatching Crystallographic Waters:

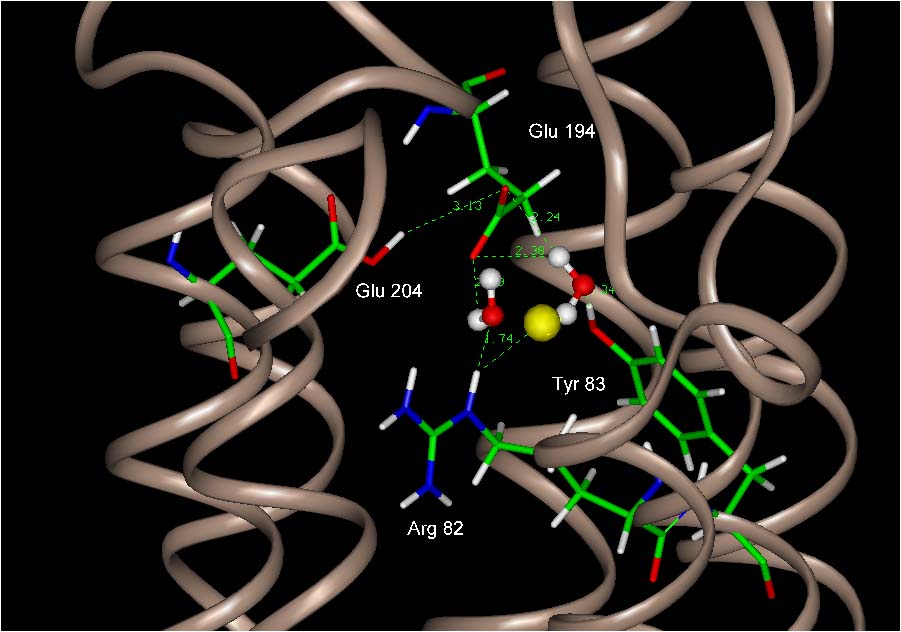
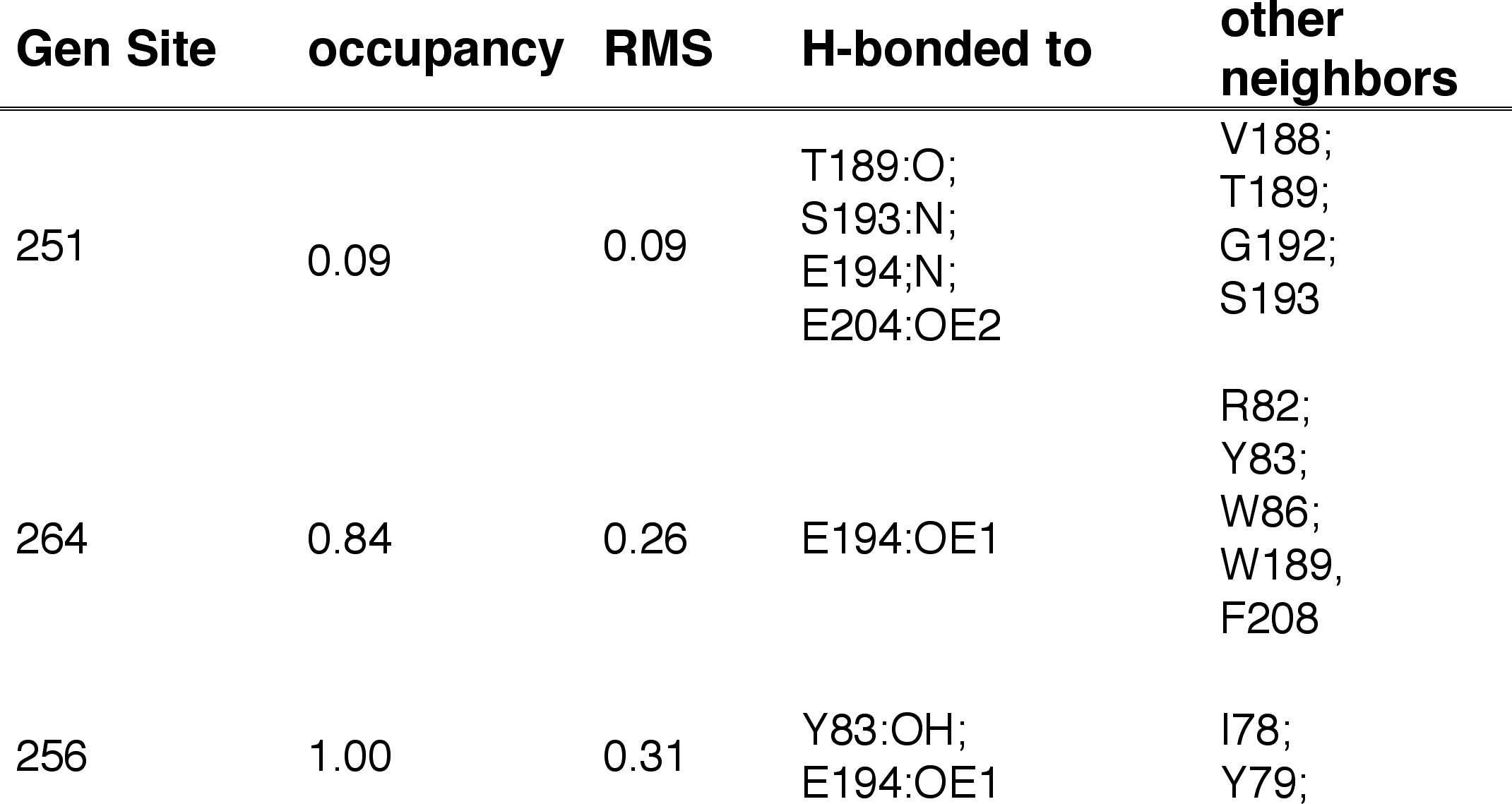
FIGURE 2: A snapshot from the simulation. BR state Crystallographic water 405 is shown in yellow. One match Simulation water 236 is to the left.  An additional match, site  256 is on the right .  Another two  nearby simulation waters, 251 and 264,  are not seen in this view, but their properties are summarized   in the table and below.
 

PROPERTIES OF ADDITIONAL WATER SITES :
 

• High occupancy sites reside in a favorable environment characterized by  intricate H-bonding network
• Lower occupancy site is in a relatively less favorable environment

CONCLUSIONS:
 

Additional waters are placed in plausible positions.

MMC is successful at locating potentially real water sites that were not observed crystallographically.
 
 

                                                                                        Table 2a:  Internal M state Generic Sites  matched to Crystallographic Waters



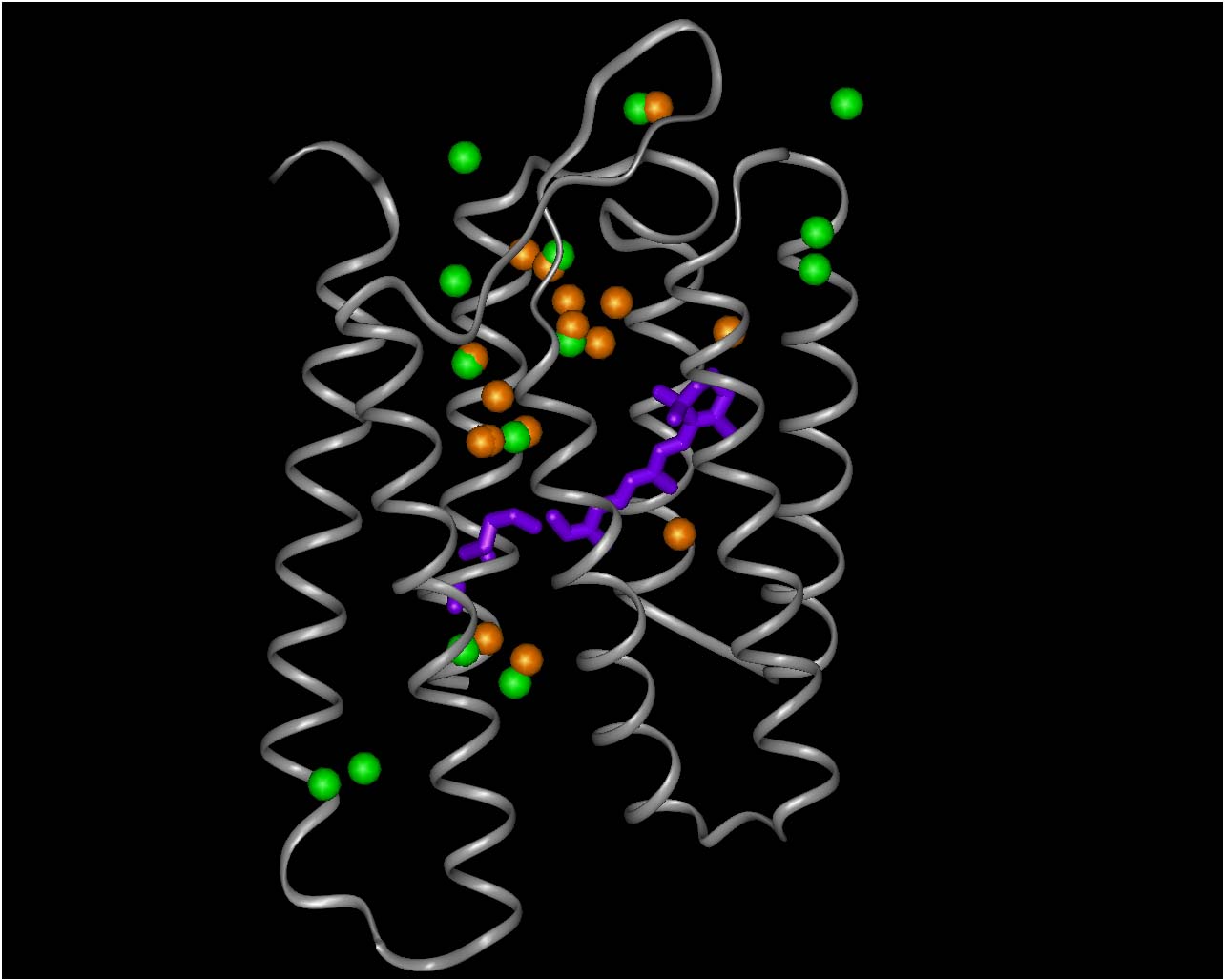
FIGURE 3:  M state crystallographic waters
in orange,  simulation waters in green
 
 
 
 

OBSERVED M CRYSTALLOGRAPHIC WATERS ARE MATCHED WELL BY SIMULATIONS AND HAVE HIGH OCCUPANCY .
 
 

ADDITIONAL M STATE SITES ARE FOUND WHICH DO NOT MATCH M STATE X-RAY WATERS:
 
 
 

Three groups: Sites that superimpose upon BR state crystallographic waters even though there are no counterparts in the M state. Sites that match to the additional sites in the BR state. This supports the assignment of the additional waters to potentially real sites. New sites in the M state that may have formed by the conformational changes in bacteriorhodopsin.


 
 

CONCLUSIONS:
 
 

1. The Grand Canonical cavity-biased Monte Carlo Method is a reliable approach for internal water localization.

2. Additional waters placed by the method in the BR state reside in an H-bonded network environment.

3. M state has the same number of internal waters as  BR state.

4. In  M state, new locations of water sites are identified, suggesting that they were formed by the conformational change in bacteriorhodopsin.
 
 
 

REFERENCES

D.J. Adams, Grand canonical ensemble Monte Carlo for a Lennard-Jones fluid, Molec. Phys., 29, 311 (1975).
 

H. Luecke,  B. Schobert, H. T. Richter, J. P. Cartailler, and Janos K. Lanyi,  Structural Changes in Bacteriorhodopsin During Ion Transport at 2 Angstrom Resolution Science,286, No 5438, 255-260 (1999)

T.J. Marrone, H. Resat, C.N. Hodge, C.-H. Chang, and J.A. McCammon, Solvation studies of DMP323 and A76928 bound to HIV protease: Analysis of water sites using grand canonical Monte Carlo simulations, Protein Science, 7, 573-579 (1998).

N.A. Metropolis, A.W. Rosenbluth, M.N. Rosenbluth, A.H. Teller, and E. Teller, Equation of state calculation by fast computing machines, J. Chem. Phys., 21, 1087 (1953).

M. Mezei, A Cavity-Biased (T,V,mu) Monte Carlo Method for the Computer Simulation of Fluids, Molec. Phys., 40, 901-906 (1980);

M. Mezei, Grand-canonical ensemble Monte Carlo study of dense liquids: Lennard-Jones, soft spheres and water. Molec. Phys., 61, 565 (1987); erratum: 57, 1207 (1989).

M. Mezei, On the Selection of the Particle to be Perturbed in the Monte Carlo Method, J. Comp. Phys., 39, 128-136 (1981).

M. Mezei, K.A. Bencsath, S. Goldman, and S. Singh, The detailed balance energy-scaled displacement Monte Carlo algorithm, Molecular Simulation1, 87 (1987).
 

H. Resat, and M. Mezei, Grand Canonical Monte Carlo Simulation of Water Positions in Crystal Hydrates. J. Am. Chem. Soc.,116, 7451-7452 (1994).

H. Resat, and M. Mezei, Grand Canonical Ensemble Monte Carlo Simulation of the dCpG/Proflavine Crystal Hydrate. Biophys. J. 71, 1179-1190 (1996).
 
 

Back to the Mezei Lab home page