| Table 1 |
 |
| rinscr and rcirc are the radii of the largest inscribed sphere and the smallest circumscribed sphere, resp.; Vcell and Vspehre are the volumes of the simulation cell and the of the sphere of radius rinscr, resp. |
Most computer simulations of condense phases employ periodic boundary conditions (PBC) to avoid the distortion introduced by surface effects. This involves surrounding recursively the basic simulation cell with replicas of itself. When the shape of the basic cell is such that these replicas don't overlap and completely fill the space then the result is an infinite system described with a limited number of degrees of freedom - those corresponding to the basic cell.
There are two kinds of artifacts the PBC introduce. The first and most obvious one is that different periodic images of an atom can get as close to each other as the diameter of the cell's inscribed sphere. The second artifact is more subtle: while the periodic system is invariant under translations, it is not invariant under rotation. Thus the fact that the regions of the cell outside the inscribed sphere is anisotropic introduces an (admittedly small) anisotropy to the system. Thus, for a system of given volume it is desirable to (a) have as large an inscribed sphere as possible and (b) have the inscribed and circumscribed spheres be as close as possible.
Initially, the ubiquitous cube was used as the simulation cell shape. This choice is easy to visualize as well as to deal with computationally. To allow the use of larger inscribed spheres with a given volume two new cell shapes have been introduced: (a) the Wigner-Seitz cell of the face-centered cubic close packing1 (FCC) since close packing ensures that this waste minimal and (b) the truncated octahedron2 (TOCT).
Interestingly, no use has been made so far of the Wigner-Seitz cell of hexagonal close packing (HCP), probably because some replica cells on different sides have different orientations thus to determine the molecule replacing the one leaving the cell may have to undergo a rotation in addition to the usual translation. It is, however implemented in the Monte Carlo program MMC3
| Table 1 |
 |
| rinscr and rcirc are the radii of the largest inscribed sphere and the smallest circumscribed sphere, resp.; Vcell and Vspehre are the volumes of the simulation cell and the of the sphere of radius rinscr, resp. |
Table 1 compares the characteristics of the cubic (CUBE), TOCT, FCC and HCP simulation cells. The comparison includes the ratio of the cell volume to the volume of the largest inscribed sphere - the closer this ratio is to one, the less the 'waste' is - and the ratio of the radius of the smallest circumscribed sphere and of the largest inscribed inscribed sphere - the closer this ratio is to one, the more `spherical' the shape of the cell is. It is clear that both indicators show the cube to be the worst. It is also clear that HCP is better than FCC since they score equally well on the inscribed sphere radius criterion, but HCP is more 'spherical' then FCC. TOCT, the most widely used cell shape, scores worse on the inscribed sphere radius test that the shapes corresponding to close-packing (as expected), but scores better than either on the test measuring the anisotropy effect.
PDB files representing the vertices of simulation cells of different shapes have been prepared with the program Simulaid4. Figure 1 shows an overlay of the four type of cells (with the same volume).
| Figure 1 |
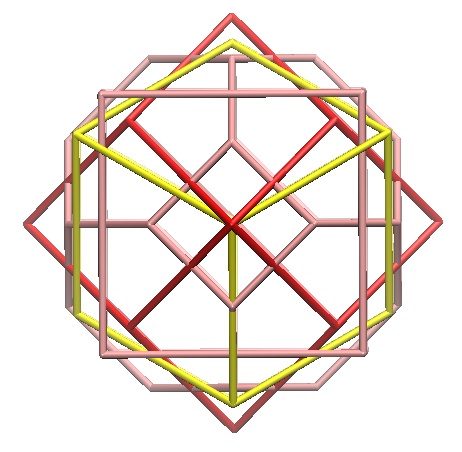 |
| Overlay of CUBE, TOCT, FCC, or HCP cells of the same volume. Gray: CUBE; red: FCC; yellow: HCP; pink: TOCT. |
Click on CUBE, TOCT, FCC, HCP to download the PDB file for CUBE, TOCT, FCC, or HCP cells, resp.
Given that the inscribed sphere 'deficit' can simply be erased by a small increase in the system size (in effect adding some more waters), but the effect of the anisotropy is much harder to estimate and it may vary from system to system, the choice of TOCT may indeed be the best among the options discussed here.
References