Gaussian Tutoral

The Gaussian Computational Chemistry Program

Adapted from http://www.chm.bris.ac.uk/pt/harvey/msci_pract/tech_g98.html

Gaussian is a complicated Fortran program which can perform a variety of computational tasks such as computing energies, optimizing geometries, computing vibrational frequencies, etc., and with a variety of computational methods, including simple Molecular Mechanics (force-field) approaches, Semi-empirical wavefunction-type methods, Hartree-Fock Self-Consistent Field methods, so-called "post-Hartree-Fock" or "correlated" methods, and Density Functional Theory approaches. Here you will learn how to:

Generate Gaussian input files.
Issue Commands to Gaussian.
Specify the Molecular Geometry.
Run a Gaussian Job.
Read Gaussian output files.

Gaussian Input Files

Gaussian input is always in the form of a unformatted text or ASCII file, usually called 'jobname'.com. For historical reasons (Gaussian has been around for more than 25 years, and new versions try to be partly compatible with older ones, so the input format has not changed much), the order of the different items in the file has to be followed very rigorously, because otherwise Gaussian does not understand the input (typically, it tries to find piece of information 'A' where you have written 'B', and that makes no sense). When this happens, the job stops, and you get a rude & incomprehensible message in the Gaussian Output (or logfile). Whenever this happens, consult the following section!!:

There are two types of lines of input in Gaussian:

Single-line Input. This is on a single, self-contained line. E.g. the 'Charge and Spin' data below.
Multiple-line Input. This is on any number of lines. For Gaussian to know where this group stops, it needs to be followed by ONE blank line. Example: the geometry specification.

Here is a sample Gaussian Input File:

The sections indicated in this file are the most common input groups. In the order in which they should appear in Gaussian, these are:

'Link 0' commands. This is the way Gaussian designates general commands concerning the way in which the program should run, what it does with files, etc. For most jobs, you will not need any Link 0 command. The line shown here, which starts with the % sign, tells Gaussian to save to your current directory the temporary 'Checkfile', and to call it ethene.chk. If you do not do this, the checkfile is kept in a temporary, 'work', directory, and deleted when the job ends. Link 0 commands are Single-line Input.

The Command Section. This is the most important part of the input: It tells Gaussian what to do ! Although it is only one line long here, it is Multiple-line Input and needs to be followed by one blank line. As with other Gaussian input, this section is case-insensitive. The first line of the Command Section needs to start with the '#' sign. Here, the program is being instructed to perform a geometry optimisation (opt) of the specified molecule, at the Hartree-Fock level of theory, and using the 3-21G standard basis set on all atoms, which it will read from its basis set library.

The Job Title. This is free for you to choose. It can be as brief or as long as you like, and may span several lines. It is multiple-line input, so it needs to be finished by a blank line. As a more verbose alternative to the dull job title I have put here, the following would be fine, too:

This file is the first Gaussian Input File I look at.
Running it will cause Gaussian to perform
an ab initio Hartree-Fock Geometry
Optimisation of the ethene molecule!!!!

The Molecular Charge and Spin setting. This begins your description of the molecule you wish Gaussian to calculate. You need to specify the overall molecular charge and the spin multiplicity (as two integers). Here, ethene is a neutral species (charge=0), and it is a spin-Singlet, with S=0 and the multiplicity, 2*S + 1, equal to 1.

The Geometry Specification. This is multiple-line input, so it needs to be followed by a blank line. Because it is often the last part of a Gaussian input file, you may forget to add a blank line, especially as with pico, you cannot see whether a blank line is there or not ! The format can be Cartesian, as here, or in Z-matrix format (see below).

Gaussian Commands

As mentioned above, the command line tells Gaussian what to do. It will generally need to specify the following things:

The theoretical method to use, including
The basis set, in most cases.
The type of job to be done, and any options chosen.

Theoretical Method and Basis Set

This is often put as the first item in the Command Section. It is written as: method/basis set. The methods you may meet include Hartree-Fock (written more simply as "HF"), MP2, the density functional theory approach called "B3LYP", or the semi-empirical "PM3" method. You will always need to specifiy a basis set, except for semiempirical computations, where no basis is needed. Basis sets you might need to use include STO-3G, 3-21G, 6-31G, 6-31+G, 6-31+G**, aug-cc-pVDZ, ... You can read about the methods and basis sets in the Ab Initio Background Section.

Job Type and Options.

If you do not specifiy anything else than the method and basis set, Gaussian will perform the default job-type, a single-point energy computation at the geometry specified. This can also be done by adding the keyword "SP". Here is a list of jobtypes you will need, and some indications on options you will need:

Single-Point Job. Keyword: SP.
Geometry Optimisation. Keyword: Opt. By default, this leads to optimisation of the nearest minimum (stable structure). This is generally trouble free. Optimising the geometry of a transition state is harder, requires you to specifiy several extra options.
Frequency Calculation. Keyword: Freq. This will calculate the matrix of second derivatives of the energy with respect to the position of the nuclei, and diagonalise it to generate vibrational frequencies. WARNING: This type of job only yields meaningful results if you have previously optimised the geometry using the same theoretical method and the same basis set. If you have not done this, you will not get a warning or error message from Gaussian, and you will apparently be able to read the frequencies in GaussView. The results will however be meaningless, as is mentioned (rather discreetly, though), in the output.
>To avoid this problem, it is probably best to use both keywords together, as in: Opt Freq. Whereas you should normally only specify one job-type, these two can be given together. Gaussian first optimises the geometry, then performs a frequency job at the optimised geometry.

Geometry Specification

There are two main ways of specifying the molecular geometry: Cartesian coordinates, and internal (or Z-matrix) coordinates. The former are more compact, but they cannot readily be set up by hand. The latter, whilst they are longer, can be used to specify any molecule's geometry in a text file. In the past, this is how the geometry of most (all !) molecules was entered into programs such as Gaussian. Nowadays, most large molecules are built using graphical programs such as GaussView, and are then saved in Cartesian or (more rarely) Z-matrix format. This is what you will do in the project about the Diels-Alder reaction. However, for the triatomic system F + H₂, Z-matrix format is simple to use and more straightforward, so it is described here.

Cartesian Geometry Specification

Geometries in Cartesian coordinates are entered simply as follows:

label1  x1  y1  z1
label2  x2  y2  z2
label3  x3  y3  z3
...

(As shown in the ethene example, above). Note that the unit of distance is Angstrom.

Z-Matrix Geometry Specification

A Z-matrix describes a geometry in terms of atom-atom distances, atom-atom-atom angles, and dihedral angles between two planes formed by four atoms. Graphically, this looks like this:

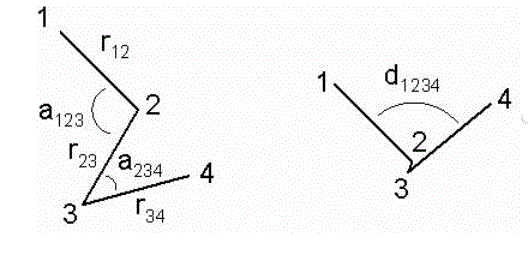
The image on the right shows the meaning of the dihedral angle d₁₂₃₄: looking down the central 2-3 bond, it is the angle between bonds 1-2 and 3-4 (this is also the angle between the planes defined respectively by atoms 1, 2 and 3 and 2, 3 and 4).

The corresponding Z-matrix would be:

 atom1
 atom2  1  r12
 atom3  2  r23  1  a123
 atom4  3  r34  2  a234  1  d1234
(atom5  4  r45  3  a345  2  d2345
   ...)

The atoms referred to in the Z-matrix do not have to be in order as shown here. To make this all a bit less abstract, here is a valid Z-matrix for H₂O:

O
H  1  0.96
H  1  0.96  2  105.

Note that the decimal point is included in the angle specification (which is in degrees). This is very important. Without the decimal point, Gaussian interprets that number as an integer, where it is expecting a real number. This will lead to rude (and incomprehensible) error messages... (yet again !)

With a dihedral angle of 0 or 180 degrees, the four atoms are coplanar. Here is an example Z-matrix for formaldehyde CH₂O:

C
O  1  1.35
H  1  1.1   2  122.
H  1  1.1   2  122.  3  180.

The numerical values for lengths and angles in the two previous examples can be replaced by variables. The value that these variables take must then be defined in a separate, multiple-lined input section situated just after the z-matrix. So the formaldehyde example above could be rendered instead as:

C
O  1  rCO
H  1  rCH  2 aHCO
H  1  rCH  2 aHCO  3  d
 
rCO  1.35
rCH  1.1
aHCO 122.
d    180.

This is what Z-matrices generated by GaussView will look like.

Running a Gaussian Job

To be able to rund a Gaussian job on Minerva, you should be a member of the Gaussian user group.

Before running a Gaussian job you have to issue the following commands (once per session):

If your default shell is bash then
csh
To make Gaussian available for your shell:
module load gaussian
followed by either

source $g09root/g09/bsd/g09.login (when your login shell is C-shell)
or by
source $g09root/g09/bsd/g09.profile (when your login shell is bash)

When you have created your input file using your favorite text editor, you should save it under the name 'jobname'.com. Then you can run the calculations, by typing:

g09 < input-file > output-file &

Reading Gaussian Output

Gaussian writes its output to a file called the logfile, which has the same name as the input file, but the '.log' extension. It writes to this file progressively as the job advances. When you open the file with a text editor, you actually open a copy of that file, so you can open the output file while the job is running to inspect the job progress, without that affecting the way the output is written. You should be very careful not to save the file if you have opened it in this way, however !!

The output is quite verbose, and the present discussion will focus on only a small part of the information you can find in the logfile.

The first few tens of lines of the output are taken up by system details and copyright information ... not very interesting !

Then you will see the following 'header':

 ***************************************
 Gaussian 98:  SGI-G98RevA.6 19-Oct-1998
                6-Sep-2000
 ***************************************

Shortly after that, your Command Section and Job Title will be echoed.

Then, you will see lots of details about your geometry. In the following block, for example, you will see the Cartesian Coordinate representation of your molecule (even if you input it as a Z-matrix):

                         Standard orientation:
 ---------------------------------------------------------------------
 Center     Atomic     Atomic              Coordinates (Angstroms)
 Number     Number      Type              X           Y           Z
 ---------------------------------------------------------------------
    1          6             0        0.000000   -0.677600    0.000000
    2          1             0       -0.924521   -1.216266    0.000000
    3          1             0        0.927705   -1.210763    0.000000
    4          6             0        0.000000    0.677600    0.000000
    5          1             0        0.924521    1.216266    0.000000
    6          1             0       -0.927705    1.210763    0.000000
 ---------------------------------------------------------------------

Note that the atoms are represented by their atomic number, not by their symbol.

Then, the calculation will start. You will see details of the initial 'guess' wavefunction which Gaussian generates, then, if all goes well, a message stating that your wavefunction has converged. This will look different for different types of job.

For a semiempirical (e.g. PM3) job, the relevant section will look as shown below. The total energy at this geometry is given by 0.174514138371 atomic units. 1 atomic unit (or Hartree) equals 2625.5 kJ/mol.

 (...)
 It=  7 PL= 4.07D-04 DiagD=F ESCF=     47.482071 Diff=-9.42D-04 RMSDP= 3.93D-05.
 It=  8 PL= 1.76D-04 DiagD=F ESCF=     47.486848 Diff= 4.78D-04 RMSDP= 2.02D-05.
 It=  9 PL= 1.17D-04 DiagD=F ESCF=     47.486816 Diff=-3.18D-06 RMSDP= 3.07D-05.
 It= 10 PL= 3.47D-05 DiagD=F ESCF=     47.486769 Diff=-4.72D-06 RMSDP= 4.50D-06.
 It= 11 PL= 1.90D-05 DiagD=F ESCF=     47.486792 Diff= 2.31D-06 RMSDP= 2.94D-06.
 It= 12 PL= 1.37D-05 DiagD=F ESCF=     47.486792 Diff=-6.30D-08 RMSDP= 5.79D-06.
 It= 13 PL= 2.30D-06 DiagD=F ESCF=     47.486790 Diff=-1.52D-07 RMSDP= 5.45D-07.
 Energy=    0.174514138371 NIter=  14.
 Dipole moment=  1.182830  0.500037  0.671478
 (...)

When you run frequencies, it will look a bit different, such as here (where the total energy is 0.103689468239 a.u.:

 (...)
 SE2nd: IAtom= 19 IXYZ=1 IS=2.
 SE2nd: IAtom= 19 IXYZ=2 IS=1.
 SE2nd: IAtom= 19 IXYZ=2 IS=2.
 SE2nd: IAtom= 19 IXYZ=3 IS=1.
 SE2nd: IAtom= 19 IXYZ=3 IS=2.
 Maximum difference in off-diagonal FC elements:
 I= 16 J=  3 Difference=    1.3800844072D-04
 Max difference between analytic and numerical forces:
 I= 17 Difference=    6.1396859930D-05
 Energy=    0.103689468239 NIter=  17.
 Dipole moment=  0.078083 -0.081208 -0.007392
 (...)

For a Hartree-Fock job, there will be a section such as the following (the energy is obvious in this case):

 (...)
 Requested convergence on             energy=5.00D-05.
 Keep R1 integrals in memory in canonical form, NReq=      468559.
 SCF Done:  E(RHF) =  -77.5985276906     A.U. after    5 cycles
             Convg  =    0.7567D-04             -V/T =  2.0034
             S**2   =   0.0000
 (...)

The output for an MP2 job is unusual, in that these jobs have two main steps: first, the Hartree-Fock wavefunction is determined, then the MP2 correction is computed. You will accordingly see output similar to the above, followed by the following, which gives the energy:
(...) Spin components of T(2) and E(2): alpha-alpha T2 = 0.5486066740D-02 E2= -0.2458707205D-01 alpha-beta T2 = 0.3482713231D-01 E2= -0.1361644265D+00 beta-beta T2 = 0.6522273303D-02 E2= -0.2267776322D-01 (S**2,0)= 0.83038D+00 (S**2,1)= 0.79224D+00 E(PUHF)= -0.10047163912D+03 E(PMP2)= -0.10065203695D+03 ANorm= 0.1023149780D+01 E2 = -0.1834292618D+00 EUMP2 = -0.10064225142696D+03 (...)
In this example, the energy (EUMP2) is -100.64225142696. Be careful not to be confused ! It is given in scientific notation, it is NOT the same as the HF energy, and there is a third energy E(PMP2) which is similar but it too is not the one you want.

After this section, the output will differ depending on whether you have asked for a geometry optimisation, a single-point, or a frequency job.

For a single-point job, or for the first step of a geometry optimisation, you will have some information on the wavefunction, e.g. the Mulliken charges, the overall dipole, etc. For the work on the Diels-Alder reaction, you will be interested in orbital energies. These are given in atomic units (Hartrees) and appear in the output in this region, in the following form:

 (...)
  The electronic state is 1-A'.
 Alpha  occ. eigenvalues --   -1.27277  -1.09035  -0.82094  -0.65970  -0.60769
 Alpha  occ. eigenvalues --   -0.49878  -0.49658  -0.46789  -0.45542  -0.40803
 Alpha virt. eigenvalues --    0.00072   0.05192   0.05756   0.07565   0.10793
 Alpha virt. eigenvalues --    0.12388   0.16303   0.18013   0.24643
 (...)

In this example, the energy of the Highest Occupied MO is -0.40803, whilst that of the Lowest Unoccupied (=virtual) MO is 0.00072.

If the job is not a geometry optimisation, this will more or less be the end of the output. If all has gone well, the ultimate lines of the logfile will be something like this:

(...)
 Job cpu time:  0 days  0 hours  0 minutes 13.3 seconds.
 File lengths (MBytes):  RWF=   10 Int=    0 D2E=    0 Chk=    5 Scr=    1
 Normal termination of Gaussian 98.

Otherwise, some or other error has occurred.

For a geometry optimisation, the energy gradient will be computed, and the geometry updated. There will be a convergence test, the results of which appear in the output as follows:

 (...)
         Item               Value     Threshold  Converged?
 Maximum Force            0.080863     0.000450     NO
 RMS     Force            0.048414     0.000300     NO
 Maximum Displacement     0.181555     0.001800     NO
 RMS     Displacement     0.173872     0.001200     NO
 (...)

All the four criteria need to be converged for the job to end. If they are not, there will be a new energy computation at the new geometry, and so on. As the optimisation proceeds, the Values should all decrease, and should start to drop below the Thresholds. Some of the 'NO's will be replaced by 'YES's. After the geometry has converged, there will be a message such as:

 (...)
 Maximum Force            0.000048     0.000450     YES
 RMS     Force            0.000013     0.000300     YES
 Maximum Displacement     0.000999     0.001800     YES
 RMS     Displacement     0.000184     0.001200     YES
 Predicted change in Energy=-1.137258D-08
 Optimization completed.
    -- Stationary point found.
                         ----------------------------
                         !   Optimized Parameters   !
                         ! (Angstroms and Degrees)  !
 ------------------------                            -------------------------
 ! Name  Definition              Value          Derivative Info.             !
 -----------------------------------------------------------------------------
 ! R1    R(1,6)                  1.3724         -DE/DX =    0.               !
 ! R2    R(1,9)                  1.087          -DE/DX =    0.               !
 ! R3    R(1,14)                 1.0957         -DE/DX =    0.               !
 ! R4    R(2,3)                  1.3856         -DE/DX =    0.               !
 (...)

The final geometry will be presented in several ways, and will be followed by the wavefunction information as mentioned above.

For a frequency job, or an optimisation + frequency job as discussed earlier, there will be a further section to the output, summarising the results of the frequency run. This will look like this:

 (...)
 Full mass-weighted force constant matrix:
 Low frequencies ---   -0.0010   -0.0008    0.0006  114.6950  189.0486  193.7753
 Low frequencies ---  929.2244 1074.4697 1116.6974
 Harmonic frequencies (cm**-1), IR intensities (KM/Mole),
 Raman scattering activities (A**4/AMU), Raman depolarization ratios,
 reduced masses (AMU), force constants (mDyne/A) and normal coordinates:
                     1                      2                      3
                    BU                     AU                     BG
 Frequencies --   929.2244              1074.4697              1114.7150
 Red. masses --     1.0406                 1.1607                 1.4837
 Frc consts  --     0.5294                 0.7895                 1.0862
 IR Inten    --     1.0153               142.6862                 0.0000
 Raman Activ --     0.0000                 0.0000                 7.4672
 Depolar     --     0.0000                 0.0000                 0.7500
 Atom AN      X      Y      Z        X      Y      Z        X      Y      Z
   1   6    -0.04   0.00   0.00     0.00   0.00  -0.08     0.00   0.00   0.15
   2   1     0.23  -0.44   0.00     0.00   0.00   0.50     0.00   0.00  -0.49
   3   1     0.23   0.44   0.00     0.00   0.00   0.49     0.00   0.00  -0.49
   4   6    -0.04   0.00   0.00     0.00   0.00  -0.08     0.00   0.00  -0.15
   5   1     0.23  -0.44   0.00     0.00   0.00   0.50     0.00   0.00   0.49
   6   1     0.23   0.44   0.00     0.00   0.00   0.49     0.00   0.00   0.49
                     4                      5                      6
                    AU                     AG                     AG
 Frequencies --  1140.4661              1385.7888              1434.9169
 Red. masses --     1.0078                 1.4914                 1.7488
 (...)
 VIBRATIONAL TEMPERATURES:   1336.94  1545.91  1603.82  1640.87  1993.83
          (KELVIN)           2064.51  2305.24  2471.81  4795.66  4817.39
                             4933.10  4974.48
 
 Zero-point correction=                           0.054602 (Hartree/Particle)
 Thermal correction to Energy=                    0.057575
 Thermal correction to Enthalpy=                  0.058519
 Thermal correction to Gibbs Free Energy=         0.033080
 (...)

This gives you the symmetry assignment of each vibrational mode, its frequency (in wavenumbers), its IR and Raman intensity, the motions of the atoms to which it corresponds, etc. It also gives you the total Zero-point energy, in atomic units, and lots of other information besides...

Last modified: 10/01/2014

Go to Mezei Lab Home page